Vertex Form

| FALL/WINTER 2023

| SPRING/SUMMER 2023

We can use the differences from a data table to determine if a equation is linear, quadratic or neither.

First Difference:

First differences are the changes in y-values for consecutive x-values in a table.

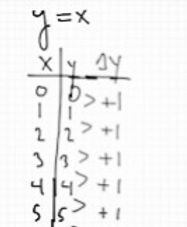
For this linear function the first differences are constent.

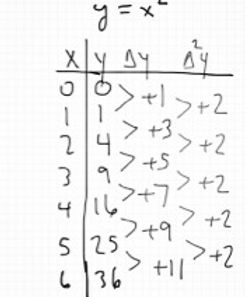
Second Difference:

Second differences are changes in the consective first differences.

Investigating Non-Linear Relationships

Charecteristics Of A Parobla

A parabola is the graph of a quadratic equation/function. It an be either in the shape of the letter 'U' or it can be in the shape of the inverted letter of 'U'.

Vertex
Y- Intercept
X-Intercept
Axis Of Symmetry
Domain and Range

Linear Relationships:

Points that follow a striaght line are known as linear relationships.

Quadratic Relationship: If points follow a curved line (parabola), the relation is quadratic.

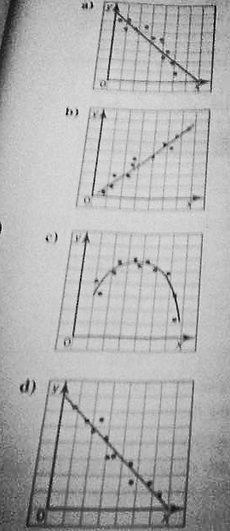
For pratice, explain whether each line of best fit is a good model for the data .Justify your answer.

Answers:

1. a) No,because the points follow a curve.

b) Yes, because the points lie close to the line.

c) Yes, because the points lie close to the curve.

d) Yes, because the points lie close to the line.

Power Of Two

When a equation is given in the form of "ax^2+bx+c", the "^2"means that it is a quadratic relation.

Investigate Transformation Of Quadratics

If the equationis given in vertex form y=a(x-h)^2+k we can explore a lot from it. Vertex form gives us the value of the axis of symmetry and the optimal value. The h values gives the axis of symmetry. The value of k gives away the optimal value. Vertex form also gives away the stretch with the factor that represents a. If the value of a is greater than 1, the parabola is vertically stretched. If the value of a is less then 1, then the parabola is horizontally compressed.

Graph y=a(x-h)^2 + k

Graphing quadratic equations can be difficult at first if the proper steps arent followed. If an equation is given in the vertex form y=a(x-h)^2+k we can discover a lot from it. Vertex form gives us the value of the axis of symmetry and the optimal value. H's sign is switched and k is taken for the axis of symentry.The value of k gives away the optimal value. After plotting the vertex one should then work towards fnding other points. Either using the step method plugging in values with one, three and five. Or making up values for the x axis plugging in the value into the equation to get the new points.

Plot The Quadratic Graph

First draw a set of axes, then plot the point of a graph, using the values of x and y from the table of coordinates of each point. For example when x=-4 y has a vlue of y=-5. This gives the coordinates of a point (-4,-5) on the graph. After plotting the points, draw a smooth line to join them.

Mapping Formula

The general mapping rule for quadratics is
(x,y) → (x + h, ay + k)
The variables a, h and k can be found in the turning point formula: y = a(x - h)² + k

Example: y=4x2+16
To get y = 4x² + 16 to turning point formula, you must complete the square
y = 4x² + 16

Divide each side by 4 to get rid of any factors before x²
y/4 = x² + 4
y/4 = (x + 0)² - 0 + 4
y = 4(x + 0)² + 16

Therefore: a = 4, h = 0, k = 16

Substitute these values into (x,y) → (x + h, ay + k)
(x,y) → (x + 0, 4y + 16)
Therefore: (x,y) → (x, 4y + 16)

This method can be applied to any other quadratic provided you know how to complete the square.

How To Write Quadratic Equations Given The Vertex And A Point

Just as quadratic equations can map a parobla, the parobla points can help write a corresponding quadratic equation. In vertex form, y=a(x-h)^2+k, the variables h and k are coordinats for the parobla's vertex. The x point sign much change though.

First substitute the vertex's coordinates for h and k in the vertex form equation. For example let use a vertex of (2,3). The equation would be y=a(x-2)^2+3.

Then substitute the point's coordinate for x and y in th equation. In this case w can use points (3,8). The new equation would be 8=a(3-2)^2+3.

After solve the equation for a. In this example solving for a would result in a becoming 5.

Lastly subsitute the values of a into the first equation. The final answer should be y=5(x-2)^2+3.

Your done, its that simple!!

Finding X- Intercepts

To find the x-intercept we set our y values to zero (y = 0) and solve for x.Then solve for x simply by using the square root principle or the quadratic formula (if you simplify the problem into the correct form).

Finding Y- Intercepts

To find the y-intercept we set our x values to zero (x = 0) and solve fory.Then solve for y by using the same square root principle or the quadratic formula.

Graphing Using The Step Pattern

Word Problems In Vertex Form

Word problems in vertex form are simple application problems given that the equation already provides information on how to solve it. Vertex form questions are usually solved using the vertex. Factored form and vertex form are alike as the methods to solve them are similar. After solving a vertex form word problem it is concluded with a defined variable or “Let” statement, work shown, solved answers and "Therefore" statement concluding your determined problem.

Vertex Form Test

Profit/ Revenue Word Problems

Profit questions are two part questions. One is for finding the selling price and maximum profit which you find simply using your vertex equation and the other is "what is the selling price if the profits are equaled to zero ?" that you can simply find by substituting "P" with zero and using reverse bedmas to solve for "S".