Quadratic Relationships Dhaval Patel MPM2D0-F
Factored Form
Factoring a quadratic equation is the second method of solving quadratic equations to which students are exposed.
If a quadratic equation in the form x2 + bx + c = 0, the factorization is in the form (x + q)(x + s), and one has to find two numbers q and s that add up to b and whose product is c. This is known as Vieta's rule.
As an example, x2 + 5x + 6 factors as (x + 3) (x + 2).
Except for special cases such as where b = 0 or c = 0, factoring by inspection only works for quadratic equations that have rational roots.
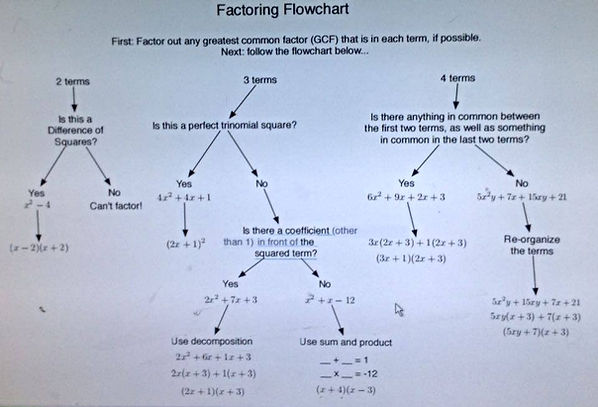
This flow chart helps understand which of the methods of factoring should be used.
.
Multiply Polynomials
Binomials are mathematical expressions made up of a variable term (x, a, 69x, 4t, 1534y) added or subtracted by a constant term (1, 2, 6666, etc.). Binomials will always contain only two terms, but they act as the building blocks of much larger and more complex equations known as polynomials.
Learn the acronym FOIL to remember the order of binomial multiplication.
FOIL stands for the order you need to multiply the parts of the binomials together: F is for First, O is for Outer, I is for Inner, and L is for Last. The names refer to the order in which the terms are written. Let's say we are multiplying the binomials (x+2) and (x+5). The terms would be:
-
First: x & x
-
Outer: x & 5
-
Inner: 2 & x
-
Last: 2 & 5
Multiply the FIRST part in each parentheses.
This is the "F" of FOIL.
In our example, (x+2)(x+5), the first terms are "x" and "x."
Multiply these together and jot down the answer: "x2."
First Term: x * x = x2
Multiply the OUTER parts in each parenthesis.
These are two outermost "ends" in our problem. So, in our example (x+2)(x+5), they would be "x" and "5." Together they make "5x"
Outer Term: x * 5 = 5x
Multiply the INNER parts in each parentheses.
The two numbers closest to the center will be your inner term. For (x+2)(x+5), this means you multiply "2" and "x" to get "2x."
Inner Term: 2 * x = 2x
Multiply the LAST parts in each parentheses.
This does not mean the last two numbers, but rather the last number in each parentheses.
So, for (x+2)(x+5), we multiply the "2" and the "5" to get "10."
Last Term: 2 * 5 = 10
Add all of the new terms together.
Combine the terms by adding them together to create a new, larger expression.
From our previous example, we get the equation:
x2 + 5x + 2x + 10
Special Products
Special Products involving Squares
The following special products come from multiplying out the parentheses . You'll need these often, so it's worth knowing them well.
a(x + y) = ax + ay (Distibutive Law)
(x + y)(x − y) = x2 − y2 (Difference of 2 squares)
(x + y)2 = x2 + 2xy + y2 (Square of a sum)
(x − y)2 = x2 − 2xy + y2 (Square of a difference)
Common Factors
The easiest way to factoring quadratic equations would be to find common factors first. The first step is to factor out the greatest common factor before applying other factoring techniques if the equation has one.
Find the largest value that can be factored from each of the elements of the expression
3x^2 + 6x=0
3x(x+2) =0
3x=0 x + 2=0
X=0 x= -2
Factoring Simple And Complex Trinomials
.
Lets factor the following expression:
X^2-5x-24
Factored Form Equation: ax^2 + bx + c
There are a couple steps on how to solve basic trinomials.
Steps:
1) Find two numbers that have a product of “c”, in this case -24. The numbers should add to give you “b”. The numbers are 3 and -8.
3+ (-8) =5
3x (-8) =-24
2) Determine the signs of “b” and “c” using the rules to evaluate a trinomial to complete your answers.
Rules:
-
If "b" is negative and "c" is positive, both "r" and "s" are negative
-
If both "b" and "c" are negative or if only "c" is negative, then most likely one of "r" and "s" is negative
-
If both "b" and "c" are positive. then both "r" and "s" are positive
The number would be 3 and -8
3) But both number in two separate parentheses with x.
(x+3)(x-8)
4) Lastly, set the equations to zero and solve to isolate for our x values.
x+3=0 x-8=0
x=-3 x=8
Complex Trinomials
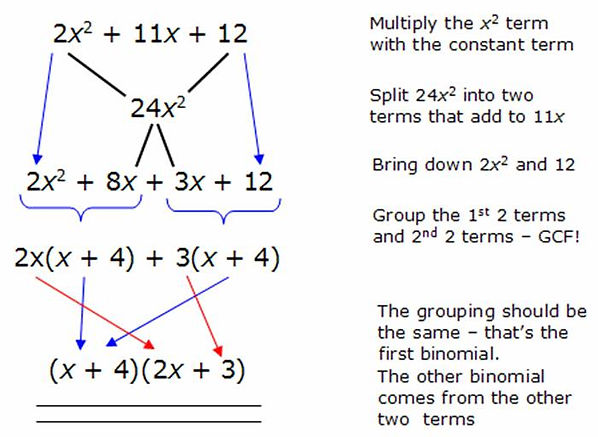
Complex trinomials will have a leading coefficient that is not 1. The same method off factoring is applied to complex trinomials as simple trinomials, but instead of finding two numbers that have a product of “c and add to give to give you “b” the “a” value is multiplied with the “c” value. Then find two numbers multiply to our new product (a x c) and add to the new product. Lets use to trinomial 6x^2 + 11x + 3.
Steps:
Step 1: First decide if the three terms have anything in common, called the greatest common factor or GCF. If so, factor out the GCF. Do not forget to include the GCF as part of your final answer.
Step 2: Multiply the leading coefficient and the constant, that is multiply the first and last numbers together. (6x3=18)
Step 3: List the factors that add to our “b” value (11) and have a product of 18. The factors would be (9 and 2)
Step 4: Rewrite the original problem with four terms by splitting the middle term (b) into the two numbers. (y=6x^2+9x+2x+3).
Step 6: Now that the problem is written with four terms, you can factor by grouping.
Y=6x^2+9x+2x+3
Y= 6x^2+2x+9x+3
Y= 2x (3x) + 3 (3x) * Note that the numbers inside the parenthesis are the always the same.
Y= (3x) (2x+3)
Factor A Perfect Square And A Difference Of A Square
Perfect Square Trinomials - (ax)^2 + 2abx + b^2. A perfect square trinomial is a quadratic that can be
factored into two identical binomials that take on the form of (ax+b)2 or (ax+b)(ax+b).
Difference of Squares – a^2 – b^2. The difference of perfect squares is when a number is
squared and then subtracted by another squared number and can be factored as (a-b)(a+b).
Differences of Squares
Factoring 9x^2 – 4
3x squares to 9x2, and 2 squares to 4, and you square to 2.
We can now take the square root terms and multiply them together as a sum and a difference.
9x2 – 4 = (3x – 2)(3x + 2)
Solve 25x2 – 36 = 0
Our square roots terms are 5x and 6, so we plug those into our differences of squares formula.
(5x + 6)(5x – 6) = 0
From here we simply find the roots for the equation.
5x + 6 = 0 and 5x – 6 = 0
X= -1.2 x=1.2
Solving Quadratics by Factoring (finding the zeros)
y = ( x - r )( x - s ) or y = ax^2 + bx + c
First factor the equation fully.
Make one side of the equation zero
0 = ( x - r )( x - s )
Set each brackets equal to zero
( x - r )= 0 and ( x - s )= 0
Solve for x
x - r = 0 ~~ x = r
x - s = 0 ~~ x = s
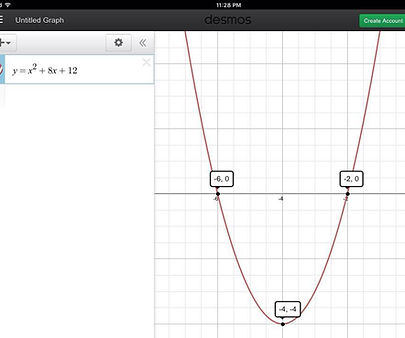
Graphing Quadratics in Factored Form

Word Problems
Dimensions of a rectangle given the area:
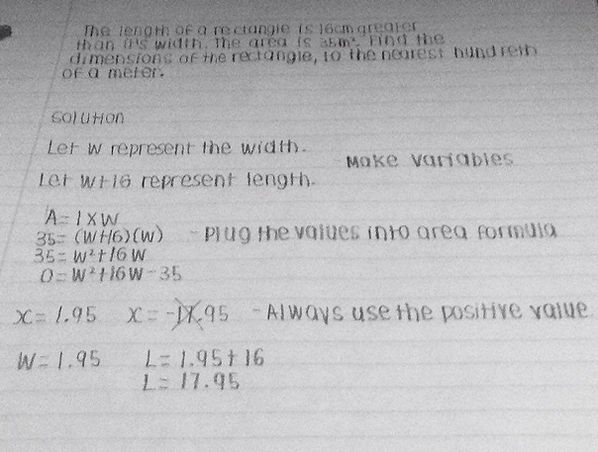
Flight Of An Object
Shaded Region Of A Shape


Factored Form Test