Standard Form

The from ax^2+bx+c=0 is called a standared form of a quadratic equation.

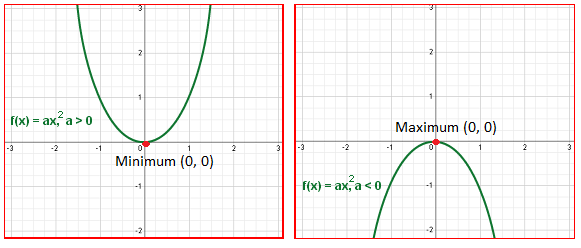
Maximum And Minimum

The y-coordinate of the parabola's vertex is also the maximum or minimum value of the quadratic function represented by the parabola.

First decide whether you’re going to find the maximum or minimum value.

The values of a quadratic function occur as its vertex.

Equation: y= ax^2+bx+c (c-b^2/4a gives you the vertex).

If the value of a is positive, you’re always going to get the minimum because the parabola opens upwards.

If the a is negative, you’re going to find the maximum value as the parabola opens downwards.

Completing The Squares

To complete the squares you must first write the equation in standard form y=ax^2+bx+c. Here are some examples I did explaning how to change from vertex form to standard.

1. Group x-terms.

2. Common factor just the value of “a” from the x-terms. Simply factor out the number in front.

3. Divide the coefficient of the middle term by two, square it, then add and subtract that number inside the brackets.

4. Remove the subtracted term from the brackets. On the way out of the brackets, it is multiplied by the “a” value that you factored out.

5. Write the perfect square trinomial as the square of a binomial

Here are some more examples!

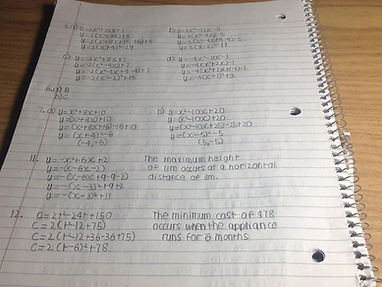
The Quadratic Formula

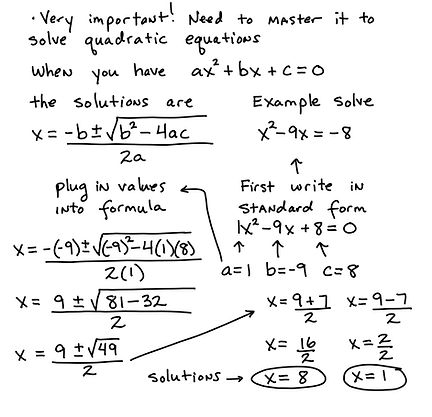
How to solve Quadratic Formula:

Steps

A standard form, ax^2 + bx + c, determines the values of a, b and c in the quadratic formula.

First plug in the values to the quadratic formula and solve using BEDMAS principles.

When done square rooting the number, separate the positive and the negative (between -b ± √) off separately to get both of the zeroes/x-intercepts.

Solve both branches and you will end up with both your x-intercepts/zeroes.

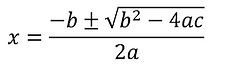
Word Problems:

Flight of an Object - Revenue problems - Consecutive integers and triangle problems - Maximum Area problems

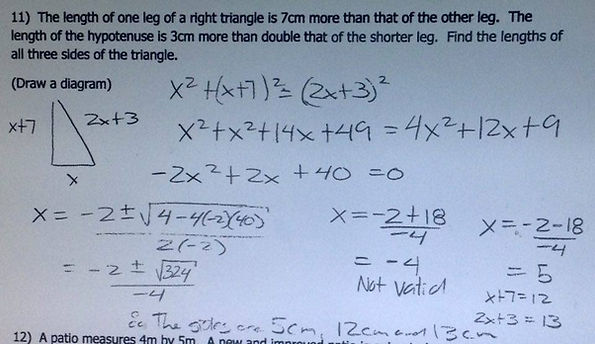
Standard Form Test

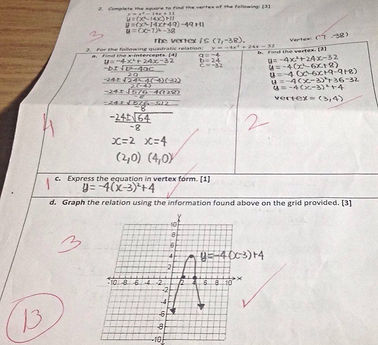
Tips

Discriminates

The discriminate can be used to determine how many solution an equation will have.

The equation for discriminate is D=b²-4ac and you substitute the values from your original equation to solve for the discriminate. If the discriminate is more than 0 that means that there will be 2 solutions. If the discriminate is 0 then there will be 1 solution and lastly if the discriminate is less than 0 there will be no solutions.

Example:

D=3²-4(2)(-5)

D=9-4(-10)

D=9+40

D=49

This means that there is 2 solutions.

D=2²-4(1)(1)

D=4-4

D=0

This means there is 1 solution

D=2²-4(5)(2)

D=4-4(10)

D=4-40

D=36

This means there are no solutions